머신러닝 - 분류 - 베이즈 정리 - 베이지안 정리

베이지안 정리
불확실성 반영 주관적 확률 이론


개념 사전확률과 우도에 의하여 사후확률을 구하는 방법
1. 사전확률 : 기 경험에 의해 얻어진 확률값
2. 사후확률 : 경험하지 않은 사건의 확률
3. 우도 : 가능성, 가능도

[배경] 동등한 비율로 확률 도출되는 동등분포이론(베르누이 무차별원칙) 기반 실제 현실에서 실험 한계
상대적 확률을 높이기 위한 시도: 상대적 빈도 확률이론, 선험적 확률이론, 주관적 확률이론
[정의] 이전의 경험과 현재의 증거를 토대로 어떤 사건의 확률의 정확도를 보정하는 방식으로 추론하는 주관적 확률이론
- 사전적 확률을 구한 후 확률에 영향을 미치는 변수의 확률을 반영하여 사후 확률을 구하는 방법으로 확률의 정확도를 높이고자 하는 주관적 확률 이론
[key]주관적 확률이론, 불확실성 추론, 사전확률, 사후확률(수정된 확률)

[단계] 하나의 가설 설정, 가설에 대한 사전적 확률 설정 
=> 과거의 통계와 측정된 데이터 반영을 통한 사전확률 보정 통계이론 
[활용] 패턴인식, 스팸메일 필터링, 실험, 예보, 품질관리, 통계적 유의성 검정 대안

 

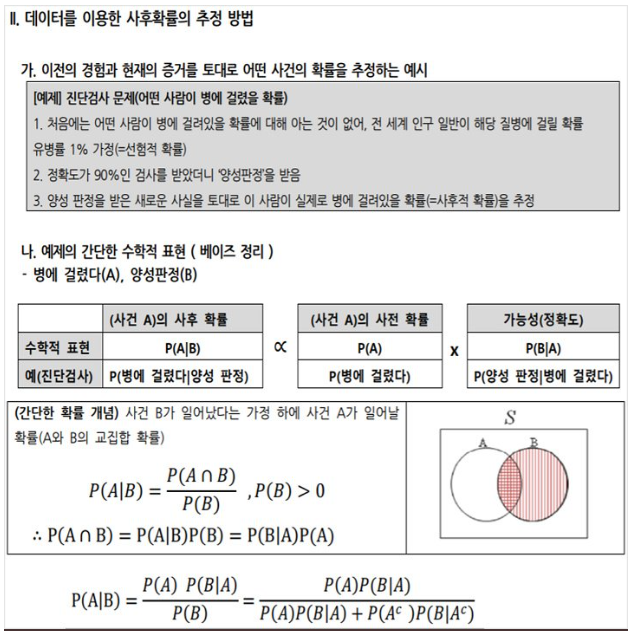
1. 처음에는 어떤 사람이 병 I에 걸려있을 확률에 대해 아는 것이 없어, 전 세계 인구 일반이 해당 질병에 걸릴 확률인 1%의 유병률을 가정했다.
2. 그런데 정확도가 90%인 검사를 받았더니 양성 판정을 받았다.
3. 이 사람이 검사에서 양성 판정을 받았다는 새로운 사실을 토대로 이 사람이 실제로 병에 걸려있을 확률을 알 수 있지 않을까?

 

베이즈 검정에서는 p 값 대신에 귀무가설과 대립가설이 참일 확률을 계산한다. 이 값들은 사용자들의 오해를 줄이고 직관적인 답을 준다. 이 외에도 이단계 검정이나, 통상적인 값보다 훨씬 작은 유의수준(p value)을 쓰는 것 등이 대안으로 제시

 

 

 

1. 베이즈 정리의 설명

가. 베이즈 정리의 정의

    - 두 확률 변수의 사전 확률(Prior Probability)과 사후 확률(Posterior Probability)간의 관계를 나타내는 확률 이론

    - n개의 서로 배반인 사건 A1, A2, ... , An 중 하나는 반드시 일어난다고 할 때, 임의의 사건 B에 의해 사건 A가

     일어날 조건부 확률

    - n개의 서로소인 사건 A1, A2, ... , An가 표본공간 S를 분할하고, 사건 A가 표본공간 S의 임의의 사건이라 할때

 

 

 

구분	설명
사전확률 (Prior Probability)	관측자가 이미 알고 있는 사건의 확률, P(A)
우도 (Likelyhood)	이미 알고 있는 사건이 발생했다는 조건 하에 다른 사건이 발생할 확률, P(B|A)
사후확률 (Posterior Probability)	사전확률과 우도를 통해 알게되는 조건부 확률, P(A|B)

 

나. 베이즈 정리의 이해를 위한 이론

 

1)전 확률의 정리

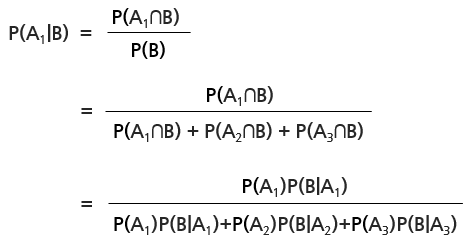
- n개의 서로소인 사건 A1, A2, ... , An가 표본공간 S를 분할한다고 할 때,     A1에 대하여 P(B) = P(B∩A1) + P(B∩A1c)  - 또는 P(B) = P(A1 ∩ B) + P(A2 ∩ B) + P(A3 ∩ B) + P(A4 ∩ B) + P(A5 ∩ B) ... + P(An ∩ B)                    = P(A1)P(B|A1) + P(A2)P(B|A2) + P(A2)P(B|A2) + ... + P(An)P(B|An)                    = ∑ P(An)P(B|An)   (단, P(Ai) > 0, i = 1, 2, ... , n)

2)확률의 곱셈정리

P(A ∩ B) = P(A) X P(B|A)

2. 베이즈 정리를 활용한 주어진 문제 풀이

가. 주어진 문제의 조건정리

 

-1학년이 30% => P(1학년)=0.3 -2학년이 40% => P(2학년)=0.4 -3학년이 30% => P(3학년)=0.3

- 1학년 중 20%가 여학생 => P(여학생|1학년)=0.2 - 2학년 중 30%가 여학생 => P(여학생|2학년)=0.3 - 3학년 중 10%가 여학생 => P(여학생|3학년)=0.1

 

나. 주어진 문제의 풀이

 

구분	설명
문제	임의로 뽑은 한 명이 여학생일때, 이 학생이 3학년일 확률
문제의 수식변환	P(3학년|여학생)
문제 풀이
답	14.3%

3. 베이즈 정리의 활용

활용	설명
스팸메일 필터링	P(스팸메일|"대출"이라는 단어)
나이브 베이즈 (Naive Bayes)	-모든 특성값은 서로 독립임을 가정 ex) 특정 과일을 사과로 분류 가능하게 하는 특성들 (둥글다, 빨갛다, 지름 10cm)은 나이브 베이즈 분류기에서 특성들 사이에서 발생할 수 있는 연관성이 없음을 가정하고 각각의 특성들이 특정과일이 사과일 확률에 독립적으로 기여하는 것으로 간주