#정의: 이진탐색과 같은 원리의 탐색구조이며, 비교적 빠른 시간안에 삽입과 삭제를 할 수 있는구조
# 이진탐색은 배열에 저장되어 삽입,삭제시 앞위의 원소를 이동시켜야 하는 불편함 있음.
>> 삽입,삭제가 빈번히 이루어지면 반드시 이진탐색트리를 사용해야 함.
#이진탐색트리 삽입과정 소스코드
typedef struct _tagNode
{
Node* parent;
Node* left;
Node* right;
Int value;
} Node;
void InsertNode(Node*& treeNode, Node* newNode) {
if (treeNode == NULL) // 탐색이 실패한 곳의 부모 노드가 null 이면 루트에 삽입
treeNode = newNode;
else if (newNode->value < treeNode->value)
// 부모노드 키값보다 작으면 왼쪽에 삽입
InsertNode(treeNode->left, newNode);
else
InsertNode(treeNode->right, newNode);
}

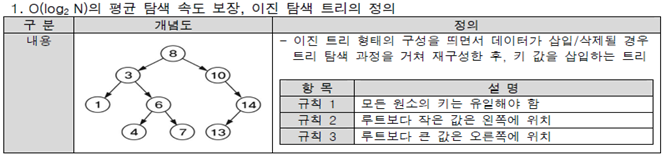
이진 트리 형태의 구성을 띄면서 데이터가 삽입/삭제될 경우트리 탐색 과정을 거쳐 재구성한 후, 키 값을 삽입하는 트리
규칙 1 )모든 원소의 키는 유일해야 함
규칙 2 )루트보다 작은 값은 왼쪽에 위치
규칙 3 )루트보다 큰 값은 오른쪽에 위치
2. 이진 탐색 트리에서의 데이터 삽입 매커니즘
가. 이진 탐색 트리에서의 데이터 삽입 알고리즘
구 분 설 명 알고리즘
1) 전체 트리에서 삽입하고자 하는 키 값이 존재하는지 탐색
2) 탐색이 성공하면 이미 존재하는 노드로 간주하고 종료
3) 탐색이 실패하면
3-1) 탐색이 실패한 곳의 부모 노드가 NULL이면 루트로 삽입
3-2) 부모 노드의 키 값과 비교하여 작으면 왼쪽, 크다면 오른쪽 자식으로 삽입탐색 방법 전위 순회 루트 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리 방향으로 모든 트리 탐색중위 순회 왼쪽 서브 트리 -> 루트 -> 오른쪽 서브 트리 방향으로 모든 트리 탐색후위 순회 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 방향으로 모든 트리 탐색- 일정한 규칙을 기반으로 트리를 탐색하여 키 값을 삽입하는 과정을 수행
[이진탐색 트리에서의 데이터 삽입 알고리즘 세부 과정]
구 분 삽입 과정 삽입 프로세스 세부 내역
Phase #1 - 삽입하고자 하는 키 값이 루트 노드의 키값보다 작으므로 왼쪽서브트리탐색
Phase #2 - Level2의 왼쪽 서브노드의 키 값과 비교
- 삽입하고자 하는 키값이 크므로 오른쪽으로탐색 진행
Phase #3 - Level 3의 오른쪽 서브노드의 키 값과 비교- 삽입하고자 하는 키 값이 크므로 오른쪽으로탐색 진행
- Level 4의 오른쪽 서브트리가 NULL 이므로노드를 생성하고 삽입 완료
3. 이진 탐색 트리의 코드 구현 사례 (C언어 기반) Node 자료 구조 삽입 코드

'08.Algorithm' 카테고리의 다른 글
| 다익스트라 (Dijkstra's) 알고리즘 (0) | 2020.06.02 |
|---|---|
| Djkstra 알고리즘과 A* 알고리즘 (0) | 2020.06.02 |
| 퀵정렬 (Quick Sort) (0) | 2020.06.02 |
| 삽입정렬 (Insert Sort) (0) | 2020.06.02 |
| 선택정렬 (Select Sort) (0) | 2020.06.02 |




