중심극한정리(Central limit theorem)에 의해 sampling distribution은 sqrt(N)에 scaled되어서(=곱해져서) Normal분포로 접근한다는 것이 알려져 있습니다. 그런데, 모집단의 분산이 알려져 있지 않은 경우에는 평균에 대한 가설검정을 할 때 Normal분포를 사용하지 않고 t-분포를 사용하는 데 이는 귀무가설이 덜(less) 기각되도록 하는 안전한 접근, 즉 보수적인(conservative) 접근이며 t-분포를 사용한다는 것은 Normal분포를 사용해 가설검정을 하는 것과 큰 차이가 있는 것은 아닙니다.
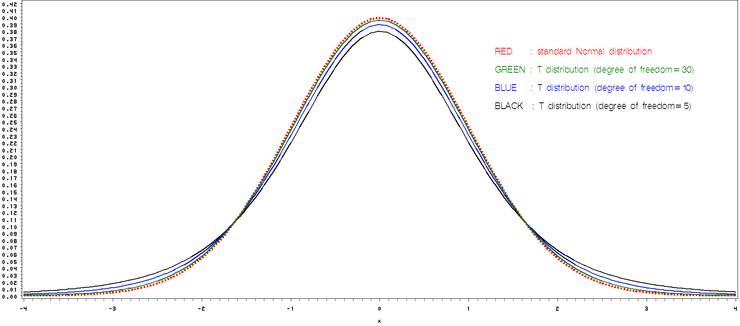
이해를 위해 t-분포와 standard Normal분포의 관계에 대해 그래프를 그려보면 다음과 같은데 자유도(=N-1)가 각각 5, 10, 30인 t-분포와 standard Normal분포의 PDF입니다. t-분포에서 자유도가 5로 작더라도 standard Normal분포에 어느정도 접근한다는 것을 알 수 있습니다. 그런데, 자유도가 작을수록 양쪽 끝부분이 standard Normal분포에 비해 두텁다는 것을 알 수 있습니다. 양쪽 끝 부분이 두터우면 기각역이 분포의 바깥쪽으로 이동하게 됩니다. 즉, 귀무가설이 그만큼 덜(less) 기각되도록 하는 것입니다. t-분포는 자유도가 100이상이면 standard Normal분포와 거의 같습니다.
자유도가 100 이상이면 2-t-rule('/two-t-rule/')이라고 하여 검정통계량의 절대값이 약 2이상이면 유의수준 5%에서 귀무가설을 기각하면 됩니다. 자유도가 100인 경우의 정확한 임계치(critical value)는 약 +-1.98인데 Ms-Excel을 사용해서 자유도가 100인 t-분포의 임계치를 구하기 위해서는 =tinv function을 사용하면 되는데 다음과 같습니다. 참고로, Ms-Excel의 function에 대한 syntax 및 의미는 keyboard의 F1버튼을 눌러서 실행시킬 수 있는 도움말 기능을 참고하세요.
=tinv(5%, 100) = 약 1.983972
'07.AI' 카테고리의 다른 글
| 모델 성능 평가 - 데이터 분류 - ROC 커브 (0) | 2024.05.14 |
|---|---|
| 데이터 분류 모델 - 혼동행렬 (0) | 2024.05.14 |
| 통계 - 기술 통계와 추론 통계 (0) | 2024.05.13 |
| LLM - 테스트 (0) | 2024.05.13 |
| LLM - 서비스 레벨 목표(SLO) (0) | 2024.05.10 |




