728x90
반응형
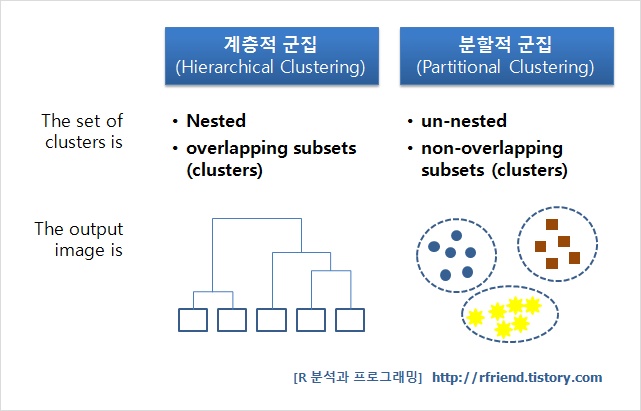
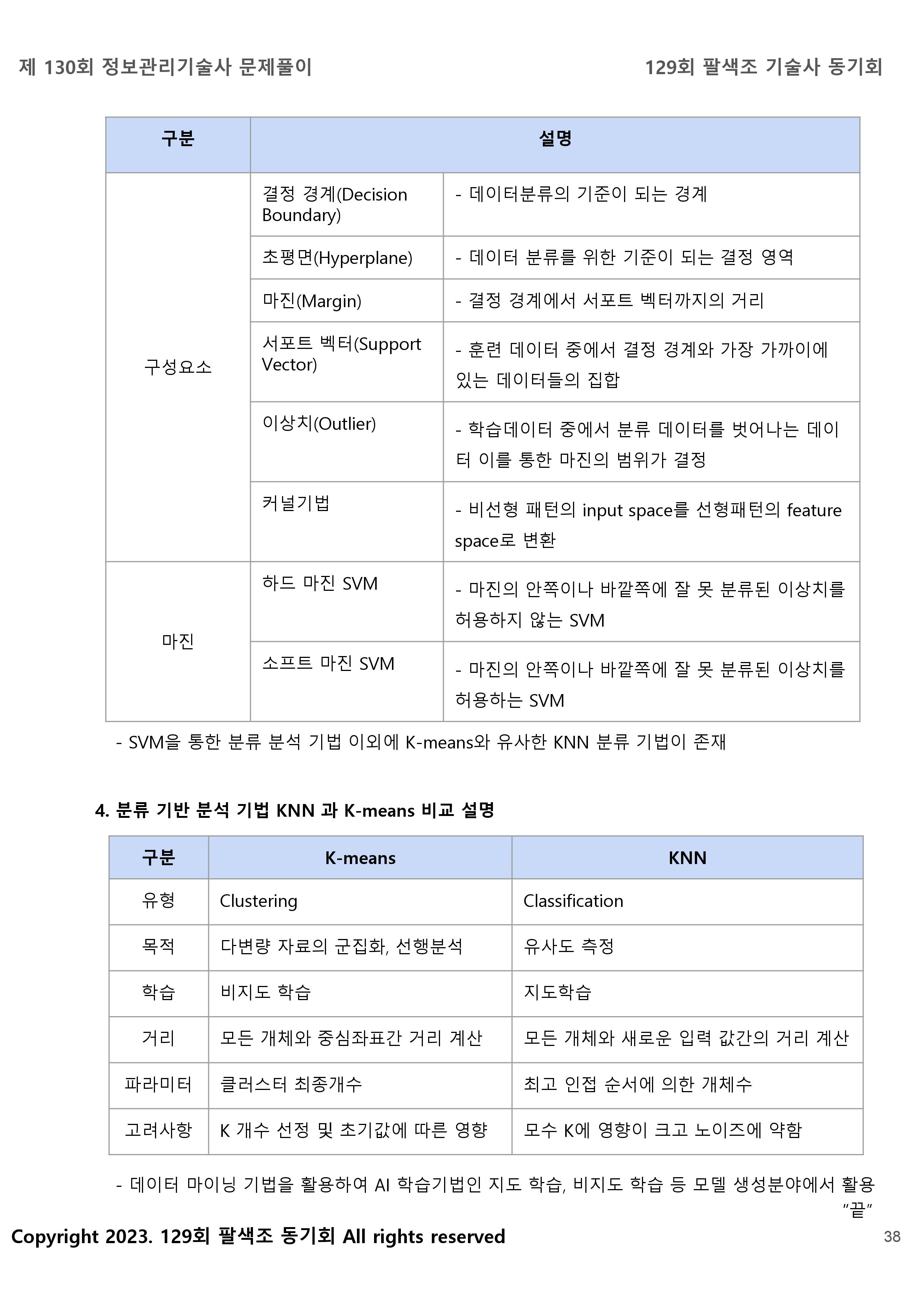
군집(Clustering)
Centeroid, 데이터군 양자화
비지도학습, distance group수거리기반 군집, 유클리디안 거리 함수
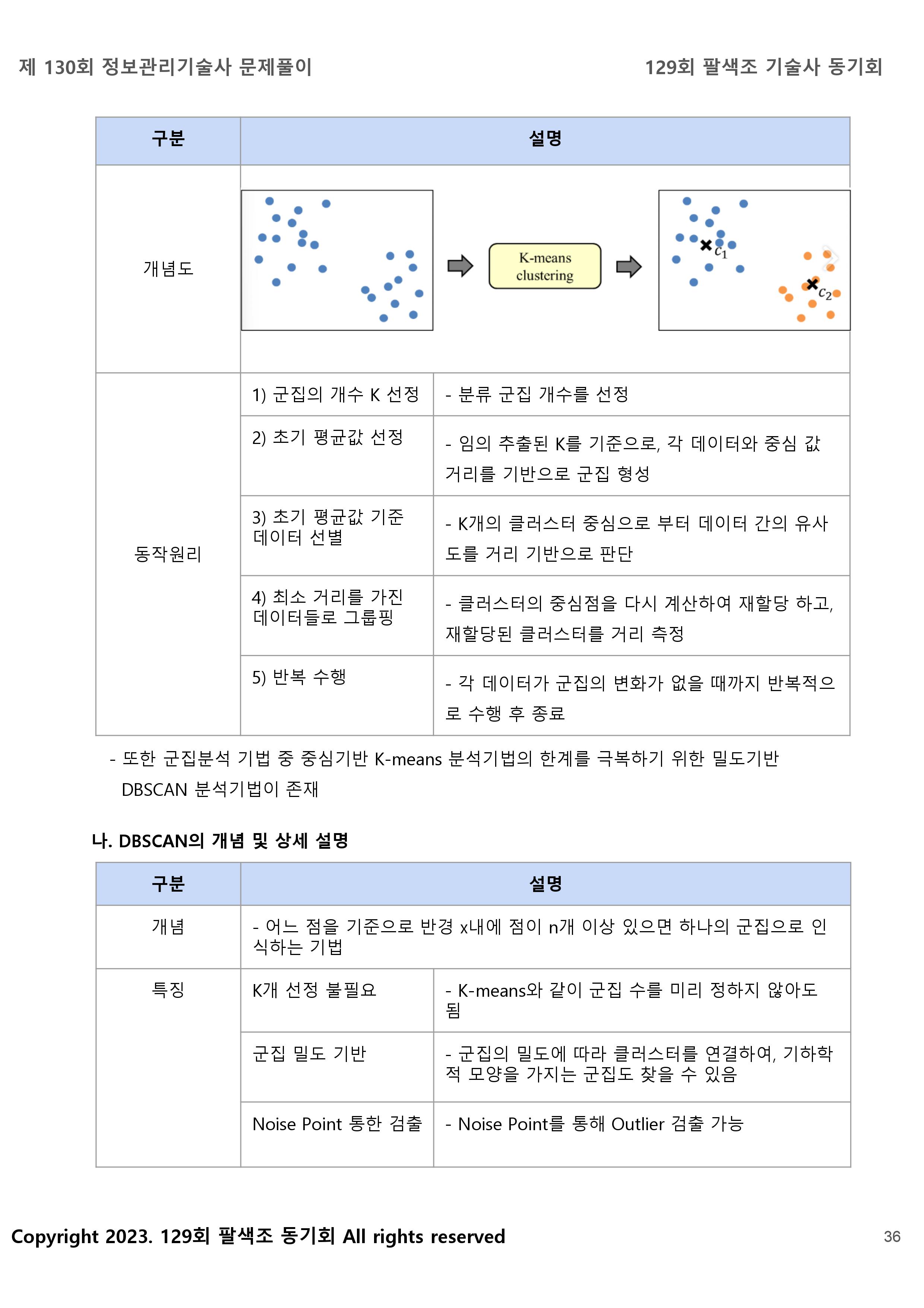
[개념] K개의 클러스터로 묶고 군집별 중심값에서 중심과의 거리를 기반으로 데이터를 분류하는 군집기법 알고리즘
- 주어진 데이터를 사전 정의된 k 개의 클러스터로 묶는 알고리즘, 각 클러스터와 거리차이의 분산을 최소화하는 방식으로 동작.
- 군집(Cluster)별 중심 값에서 중심과의 거리를 기반으로 데이터를 분류하는 군집 기법의 종류
- 입력 값으로 K 를 취하고 군집 내 유사성은 높게, 군집간 유사성은 낮게 되도록 N 개의 객체집합을 K 개의 군집으로 군집하는 기법
[K-means 알고리즘의 특징]
1)Data 중심점(Centeroid) -군집화된 데이터는 중복되지 않으며 상호배타적 포함
2)거리 기반의 분류기법 -각 군집의 중심점과의 유클리디안 거리 최소화
3)데이터군 양자화 -데이터군을 양자화하여 분할 시 발생하는 오류 최소화
4)속도 및 구현 -거리기반의 군집기법으로 빠른 결과 산출, 구현 용이성
- 군집 갯수가 사전에 정의되고, 거리계산이 가능한 Data만 적용
- 간단한 구조, 많은 환경에서 빠르게 수렴(처음 주어진 데이터 개수보다 적은 반복 필요)
- 전역 최적값을 보장하지 않음(맨 처음 K 값에 따라서 실제 최적값보다 나쁜 값이 나올 수 있음)
[K-means 절차]
1. 각 센트로이드 위치에 근접한 점들 특정 군집 할당
2. 군집의 모든 점을 좌표 평균 계산
1 군집의 수 K 를 정의
2 초기 K 개 군집의 중심(Centroids) 선택
3 각 관측 값들을 가장 가까운 중심의 군집에 할당
4 새로운 군집의 중심 계산
5 재정의 된 중심값 기준으로 다시 거리기반의 군집 재분류
6 군집 경계가 변경되지 않을 때까지 반복
[고려사항]
- 초기 클러스터 설정 의존적. 전역 최적값 보장하지 않음 -> 서로 다른 초기값으로 여러 번 시도
- 클러스터의 개수 제한 필요
- 거리측정 통한 마탈로노스, 코사인 유사도 활용가능






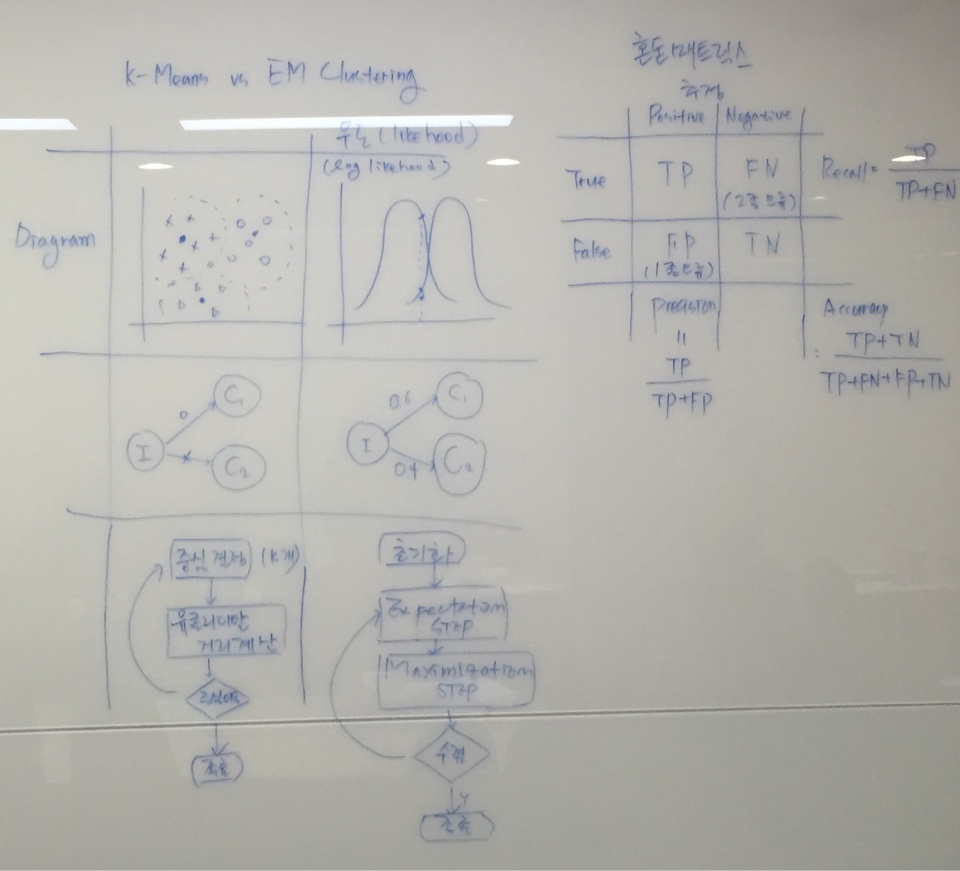
가. K-Means 알고리즘과 EM 클러스터링 알고리즘의 비교
나. K-Fold Cross Validation
1. 동질 데이터끼리 군집, 클러스터링 기법의 개요
가. 클러스터링 기법의 개념 및 특징
- 개념 : 데이터가 속해 있는 군집을 모르는 상태에서 유사한 혹은 동질의 데이터끼리 군집으로 묶어 주는 분석 기법
- 특징 : 결과값에 라벨이 없는 상태로 진행, 초기 탐색적 분석 단계 활용, 기계학습/데이터마이닝/통계등 다양한 분야 활용
나. 군집화의 원리 및 유형
- 원리 : 군집 내 응집도 최대화/ 군집 간 분리도 최대화 관련 설명
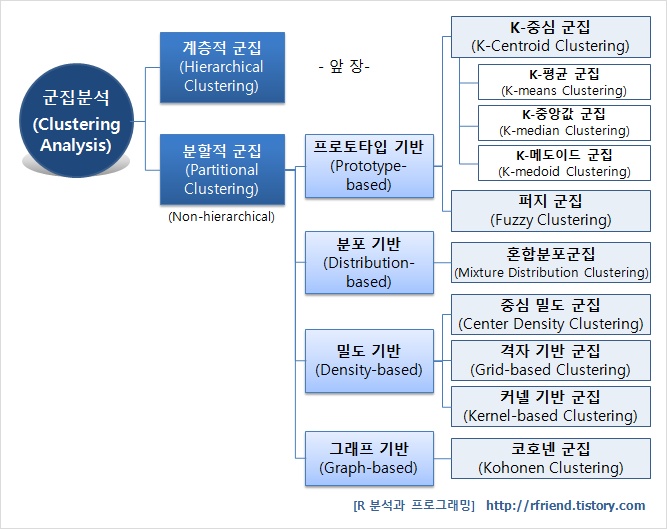
- 유형 : 계층적 군집(단일,완전,평균,와드방식)/비계층적 군집(K-means외 클러스터링) 간략 설명
- 비지도 학습에서 군집을 명확히 묶기 위해 일반적으로 K-means와 EM clustering 기법 사용
2. K-means 알고리즘과 EM 클러스터링 알고리즘의 비교 설명

가. K-measn와 EM 클러스터링의 원리론적 비교
- 개념과 유클리디안/확률밀도 기반에 대한 설명
나. K-measn와 EM 클러스터링의 군집 확정 process 기반 비교
- 앞에서 설명한 원리를 그림으로 표현하여 설명
다. K-measn와 EM 클러스터링의 세부 비교
- 특징, 장점, 단점, 활용사례 등으로 비교
- 비지도학습에서 데이터 셋을 이용한 알고리즘 학습 시 여러가지 특성(데이터 모수, 활성화함수 종류 등)에 따라 과적합에 빠지기 쉽고 해당 모델이 학습한 내용에 대한 평가가 중요함. 보통 10단계의 K-Fold Cross Validation 이용
3. K-Fold Cross Validation의 설명
가. K-Fold Cross Validation의 개념적 설명
- K-Fold Cross Validation의 개념 설명
나. K-Fold Cross Validation 활용한 프로세스 설명
- 그림통한 프로세스 설명
다. K-Fold Cross Validation을 이용한 효과 설명
- 모델 성능관련한 설명과 데이터 모수 부족등인 경우 Bootstrap등을 효율적으로 동시 수행하는 것에 대한 설명
- 현재까지 설명을 통해 비지도학습의 대표적인 알고리즘과 모델 성능에 대한 기본적인 이해가 가능하고, 실제 비지도 학습을 통한 클러스터링 구현시에는 추가적으로 고려해야 할 부분들이 존재.
4. 클러스터링을 이용한 비지도 학습 구현 시 추가 고려사항
- 군집화 변수 특징, 군집분석과 요인분석 비교 수행, 사용 변수 표준화, 군집 수 결정(덴 다이어그램 이용), 변수 척도의 기준, 사용 변수와 변수의 가중치 등을 적절한 그룹핑을 통해 설명
- Backpropagation의 문제점을 해결하기 위한 RBM과 RBM을 적층한 DBN은 현재 인공지능 제 3의 중흥기를 이끌고 있음. 제 4차 산업혁명으로 대변되는 ICT 지능산업에 대비하기 위해 정부 차원 응대로 국가 경쟁력 필요함. "끝"
I. 인공지능 비지도 학습 발달에 따른 클러스터링 기법에 대한 관심과 활용도 증대
- 비지도 학습 개념 : Class / Label이 없는 Training Set으로 학습하며, 주로 군집을 목적으로 하는 학습
- 비지도 학습 주요 기능 :
-. 군집화 ( Clustering) : k-means, EM Clustering, Dendrogram Clustering
-. 잠재변수 모델 : Principal Component Analysis, Restricted Boltzman Machine
=> 비지도 학습의 주요 기능은 군집화 기능으로 대표적 알고리즘으로 K-means와 EM Clustering이 존재
II. K-means 와 EM Clustering 비교
K-means EM
개념 - 강한 군집화 - 약한 군집화
- Euclidean 거리 기반 - 확률밀도 기반
장점 - 구현 용이 - Outlier와 noise에 강함
- 직관적인 이해 가능 - 중첩된 군집을 구분
약점 - outlier와 noise에 약함 - 정규분포를 따르지 않은 밀도를 갖는 군집은 구분 가능
- 중첩된 군집을 구분 - 구현이 복잡
=> 학습에 의한 결과가 얼마나 목표에 부합하는지 측정하고 수치로 제시하기 위하여
k-fold cross -validation 사용 가능
III. 객관적인 모델 성능 평가를 위한 k-fold cross validation
가. k-fold cross-validation 개념 및 특징
: 원시 Data Set에서 Training Set, Validation Set, Test Set에 속한 원소를 K회 바꿔서
성능을 검증하는 방법( Random 추출, 구간 추출 )
나. k-fold cross-validation 예시
IV. clustering이 적용된 대표적인 알고리즘
Clustering을 기반으로 추천엔진을 제공하는 Mahout에는 다양한 알고리즘 적용
- Canopy
- k-means fuzzy k-means
- Mean-shift
- dirichlet
-> Clustering을 기반으로 빅데이터 및 다양한 분야에 활용됨
두 가지 방법의 차이점은 클러스터 모델입니다. Fuzzy C-means와 K-means는 클러스터를 원형 (n 차원 공간의 구)으로 모델링하고, EM 클러스터링은 클러스터를 확률 밀도 함수 (PDF)로 모델링합니다. 유클리드 공간에서 후자는 공분산 행렬에 의해 결정되는 타원형 (가우시안 PDF를 사용)을 가질 수 있습니다.
따라서 K-means에 대한 할당 기준은 중심점까지의 거리이며 EM 알고리즘에 대한 기준은 클러스터 중심점의 PDF로 주어진 데이터 점의 확률입니다.
K-means의 클러스터 센터는 퍼지 C에서 하드 할당됩니다. 당신이 말했듯이 주어진 데이터 포인트에 대해 가장 높은 확률 / 최소 거리로 클러스터를 선택하는 것은 어려운 결정입니다.










728x90
'07.AI' 카테고리의 다른 글
| 머신러닝 - 분류 - SVM (Support Vector Machine) 알고리즘 (1) | 2023.11.14 |
|---|---|
| 머신러닝 - 군집 - DBSCAN (1) | 2023.11.14 |
| 음성인식 - 서비스 - 챗봇 (Chatbot) - 차세대 챗봇 (1) | 2023.11.14 |
| 음성인식 - 서비스 - 챗봇 (Chatbot) (1) | 2023.11.14 |
| 통계 - 베르누이 분포와 기하 분포 (0) | 2023.11.13 |




